Question: Given a positive integer, print the next smallest and the next largest number that has the same number of 1 bit in their binary representation.
We can solve this problem using three ways. We will go through each of them here. Our upcoming section will be classified as such the following.
- Brute Force Approach
- Brute Force Approach to Get Next Number
- Brute Force Approach to Get Previous Number
- Bit Manipulation Approach
- Bit Manipulation Approach to Get Next Number
- Bit Manipulation Approach to Get Previous Number
- Arithmetic Approach
- Arithmetic Approach to Get Next Number
- Arithmetic Approach to Get Previous Number
Related: Python Program to Count number of bits to be flipped to convert A to B
Brute Force Approach
The Brute Force Approach is the easiest way to solve the given problem. Before moving to the Optimal Solution, let's get a little intro with two Python Programs where the Brute Force method has been applied to get the Next and Previous Numbers.
Brute Force Approach to Get Next Number
The logic is too simple. Have a look at the steps below that we need to follow.
1. Count the number of ones (1s) in the given positive integer number and store it in a variable.
2. Run a while loop till the True condition.
3. Increment the current number by one.
4. Count again the number of ones (1s) in the current number.
5. If the number of ones in the given number matches with the current number, the program will return the current number as a result.
Let's implement this logic through a Python Program.
Code
'''Python Program to get the next number of the given number that has the
same number of 1s - Brute Force Approach'''
def countOnes(num):
count = 0
while num:
count += num & 1
num >>= 1
return count
def getNext(num):
countGivenNum = countOnes(num)
n = num
while True:
n += 1
if countOnes(n) == countGivenNum:
return n
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Number: ", nextNum)
Output
Please Enter the Number: 8888
Next Number: 8899
Brute Force Approach to Get Previous Number
The logic for this approach is almost the same as the previous one; just, in this case, we will decrement the given number by one in Step 3. Below is the implementation by programming.
Code
'''Python Program to get the previous number of the given number that has the
same number of 1s - Brute Force Approach'''
def countOnes(num):
count = 0
while num:
count += num & 1
num >>= 1
return count
def getPrevious(num):
countGivenNum = countOnes(num)
n = num
while True:
n -= 1
if countOnes(n) == countGivenNum:
return n
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrevious(num)
print("Previous Number: ", prevNum)
Output
Please Enter the Number: 8888
Previous Number: 8884
Bit Manipulation Approach
We will divide this discussion into two parts. The First will be for getting the next number that has the same number of 1 bit in its binary representation, and the second part will be for getting the previous number using the same approach.
Bit Manipulation Approach to Get Next Number
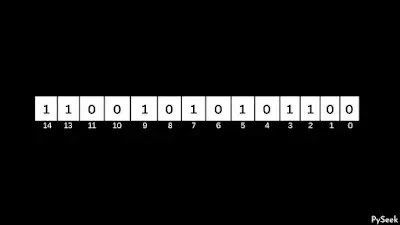
To understand the overall discussion better, we will take this positive integer number, 12972 as an example. We want the next number with the same number of 1s.
 |
| Binary representation of the given number |
You need to observe: Given number n, and the locations of two bits, i and j. Suppose we flip the bit at position i from 1 to 0, and the bit at position j from 0 to 1. If i>j, the given number n, will have decreased. If i<j, the opposite scenario will happen.
Keep in Mind
1. If we flip a bit from zero to one, we must flip another bit from one to zero.
2. If we do that, the number will be bigger if and only if the zero-to-one bit is to the left of the one-to-zero bit.
3. We want the next larger number, not unnecessarily bigger.
We will follow a few steps to get our desired result.
Step 1: Flip the rightmost non-trailing zero
See, in the above example, the rightmost trailing zeros are in the 0th and 1st position and the position of the rightmost non-trailing zero (zero followed by 1) is 4. We will call this position, p.
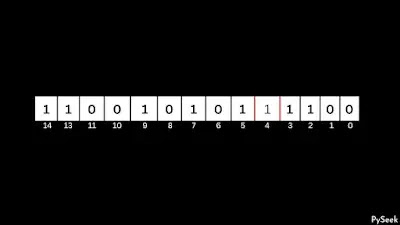
Now we will flip p zero-to-one.
 |
| Flip the rightmost non trailing zero |
Look, with this change, the size of n has increased. Now we need to shrink the size of n. Before that here, we will count count0 (number of zeroes after p) and count1 (number of ones after p).
Let's see what we get: count0=2, count1=2, p=4
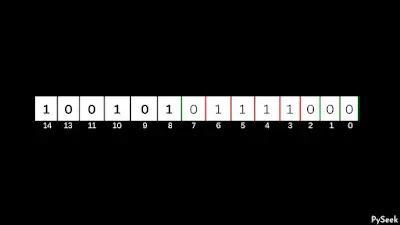
Step 2: Clear bits to the right of p
Here, we will clear all the bits (set to zero) to the right of p and see what we get.
 |
| Clear all the bits to the right of p |
Step 3: Add (count1-1) number of ones (1s) on the right side
After adding (count1-1) number of ones on the right side, we will get our final result which is the next bigger number of the given number n with the same number of 1s in its binary representation.
 |
| Add (count-1) number of ones to the right side |
The above logic is implemented by the following Python program.
Code
'''Python Program to get the next number of the given number that has the
same number of 1's'''
def getNext(num):
c = num
count0 = 0
count1 = 0
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
# If num == 11..1110...00, then there is no bigger
# number with the same number of 1s.
if count0 + count1 == 31 or count0 + count1 == 0:
return -1
# Position of rightmost non-trailing zero
p = count0 + count1
# Flip the rightmost non-trailing zero
num |= (1 << p)
# Clear all bits to the right of p
num &= ~((1 << p) - 1)
# Insert (count1-1) ones(1s) on the right
num |= (1 << (count1 - 1)) - 1
return num
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Number: ", nextNum)
Output
Please Enter the Number: 12972
Next Number: 12977
Bit Manipulation Approach to Get Previous Number
In this case, the logic is very similar to the previous one but minor difference. Here, we will take another number, 9607 as an example. We want the previous number with the same number of 1s.
You need to observe: Given number n, and the locations of two bits, i and j. we flip the bit at position i from 1 to 0 and the bit at position j from 0 to 1. In this case, i>j.
We will go through the below steps to get our desired result.
Step 1: Compute Initial Numbers
First, we need to compute count1 (number of trailing ones), count0 (size of the block of zeros just to the left of the trailing ones), and p which is the rightmost non-trailing one (one followed by 0). We can get p this way, p=count0+count1.
 |
| Binary representation of a positive integer number |
According to the above example, we get count1=3, count0=4, and p=7.
Step 2: Clear all the bits through p
After this operation, the binary representation will look like the following.
 |
| Clear all the bits through p |
Step 3: Add count1+1 number of ones just after to the right of p
After doing this we will get our desired result.
 |
| Add (count+1) number of ones just after the p |
We got our answer. Let's see the programming implementation.
Code
'''Python Program to get the previous number of the given number that has the
same number of 1's'''
def getPrev(num):
c = num
count0 = 0
count1 = 0
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
if c == 0:
return -1
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Position of rightmost non-trailing one
p = count0 + count1
# Clear all bits to the right of p
num &= ((~0) << (p + 1))
# Sequence of (coun1+1) ones
mask = (1 << (count1 + 1)) - 1
num |= mask << (count0 - 1)
return num
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrev(num)
print("Previous Number: ", prevNum)
Output
Please Enter the Number: 9607
Previous Number: 9592
Arithmetic Approach
Here, we will solve the same problem but using the arithmetic methods. As in the Bit Manipulation part, here we will create two programs separately to get the next and previous numbers.
Arithmetic Method to Get Next Number
Remember the steps we followed in the bit manipulation approach to get the bigger number. The summary looks like the following.
Step 1: Set the rightmost non-trailing zero (or p) to 1.
Step 2: Clear all the bits to the right of the p.
Step 3: Add (count1-1) number of ones (1s) on the right side.
Did you know that all the above steps can be performed in another way?
A quick way to perform Step 1 and Step 2 is to set trailing zeros to 1 and add 1 to the number.
Let's understand it through an example.
Assume, n=1010101100. We set trailing zeros to 1. Now, n=1010101111.
Next, we add 1 with n. Now, n=1010110000.
We can perform these two steps arithmetically.
n = n + (2^count0) - 1 # Sets trailing 0s to 1, giving us p trailing 1s.
n = n + 1 # Flips first p 1s to 0s, and puts a 1 at bit p.
Now, we just do the following to perform Step 3 arithmetically.
n = n + (2^(count1-1)) - 1) # Sets trailing (count1 - 1) zeros to ones (1s)
If we reduce the entire math, it would be like this,
nextNumber = n + ((2^count0) - 1) + 1 + (2^(count1-1)) - 1)
= n + (2^count0) + (2^(count1-1)) - 1
Let's move to the Python Program
Code
'''Python Program to get the next number of the given number that has the
same number of 1's - Arithmetic Approach'''
def getNext(num):
c = num
count0 = 0
count1 = 0
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
# If num == 11..1110...00, then there is no bigger
# number with the same number of 1s.
if count0 + count1 == 31 or count0 + count1 == 0:
return -1
# Position of rightmost non-trailing zero
p = count0 + count1
return num + (1 << count0) + (1 << (count1 - 1)) - 1
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
nextNum = getNext(num)
print("Next Number: ", nextNum)
Output
Please Enter the Number: 684
Next Number: 689
Arithmetic Method to Get Previous Number
If you remember the steps we followed in the bit manipulation approach to get the previous number, we took count1 as the number of trailing ones, count0 as the size of the block of zeros just to the left of the trailing ones, and p=count0+count1. Here, we will also keep the scenario as it is.
Now if I summarize the steps from there, it would be as follows.
Step 1: Set the bit at position p to 0.
Step 2: Clear all the bits to the right of p.
Step 3: Add count1+1 number of ones just to the right of p.
As I mentioned in the previous section, these steps can be performed arithmetically also.
Assume, n=1010100011. According to this example, count1=2, count0=3.
Clear trailing ones. Now n is 1010100000
Arithmetically: n = n - (2^count1) - 1
Flip trailing zeros. Now n is 1010011111
Arithmetically: n = n-1
Flip last count0-1 1s. Now n is 1010011100
Arithmetically: n = n - (2^(count0 - 1) - 1)
If we reduce the entire math, it would be like this,
prevNumber = n - ((2^count1) - 1) - 1 - (2^(count0 - 1) - 1)
= n - (2^count1) - (2^(count0 - 1)) + 1
Let's move to the Python Program
Code
'''Python Program to get the previous number of the given number that has the
same number of 1's - Arithmetic Approach'''
def getPrev(num):
c = num
count0 = 0
count1 = 0
# Computing count1: Number of ones to the right of p
while ((c & 1) == 1):
count1 += 1
c >>= 1
if c == 0:
return -1
# Computing count0: Number of zeros to the right of p
while (((c & 1) == 0) and (c != 0)):
count0 += 1
c >>= 1
# Position of rightmost non-trailing one
p = count0 + count1
return num - (1 << count1) - (1 << ( count0 - 1)) + 1
if __name__ == "__main__":
num = int(input("Please Enter the Number: "))
prevNum = getPrev(num)
print("Previous Number: ", prevNum)
Output
Please Enter the Number: 675
Previous Number: 668
Reference
Cracking the Coding Interview (Bit Manipulation, Problem #5.4)
Book by Gayle Laakmann McDowell
Summary
In this tutorial, we solved a bit manipulation problem using python programming. The task was to find the next and the previous number of the given number which has the same number of 1 bit in their binary representation.
We tried three approaches here to solve the given problem (Brute Force Approach, Bit Manipulation Approach, and Arithmetic Approach). If you have any doubt regarding this topic, let me know in the comment section. You will get a reply soon.
Have a nice day ahead, cheers!
PySeek